General Report on Tunny
22X Page 75
(F.T.) of F is defind as the function F* where
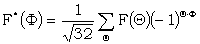 |
(X2) |
where Θ.Φ is the scalar product of Θ and Φ when they are considered as vectors with 0 for dot and 1 for cross. For example (U.N.) = 1.0+1.0+1.1+0.0= 1. It can easily be shown that F** = F, i.e. that F is the F.T. of F*, so the relation between F and F* is symmetrical.
The "Faltung", F, of two functions F1 and F2 is defined by the equation
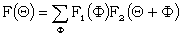 |
(X3) |
which is clearly also equal to 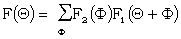 .
.
It is easy to see that if F is the Faltung of F1 and F2 then F* = 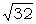 F1*.F2*. In other words the F.T. of a Faltung is
F1*.F2*. In other words the F.T. of a Faltung is 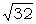 times the product of the F.T.'s. Therefore, by equation (X1)
times the product of the F.T.'s. Therefore, by equation (X1)
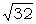 .P.B.*(ΔD) = P.B.*(ΔP) P.B.*(ΔΨ') .P.B.*(ΔD) = P.B.*(ΔP) P.B.*(ΔΨ') |
(X4) | |
| (see foot-note). | ||
where P.B.* means the Fourier Transform of the Proportional Bulge.
This gives P.B.*(ΔP) in terms of P.B.*(ΔD) and P.B.*(ΔΨ') and hence P.B.(ΔP) in terms of P.B.(ΔD) and P.B.(ΔΨ'). The process is not as laborious as it sounds in virtue of the rather simple interpretation of an F.T. For example if Θ is the T.P. letter J or vector (1, 1, 0, 1, 0) and if F is a P.B. function, taken as P.B.(ΔD) for definiteness, we have
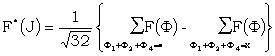 |
||
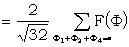 |
since F is assumed to be a P.B. function.
Thus P.B.*(J) = 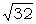 P.B.(ΔD1+2+4 = .) P.B.(ΔD1+2+4 = .) |
(X5) |
so we see that the F.T. of a P.B.is 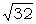 times the P.B. of the so-called "32-combination count" (R3 p. 49; R5 p. 55), for which the lower half of the Colossus switchboard is well adapted. The equation (X4) is now seen to express the well known and elementary property of the multiplication of P.B.'s.
times the P.B. of the so-called "32-combination count" (R3 p. 49; R5 p. 55), for which the lower half of the Colossus switchboard is well adapted. The equation (X4) is now seen to express the well known and elementary property of the multiplication of P.B.'s.
Observe that P.B.(ΔP) is not quite determinate since
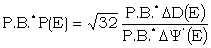 |
and the expected values of both numerator and denominator of this are zero, if ab=½. The same applies to the arguments 4, 9, 3, T.
Note: P.B.(ΔP) is a function of Θ and should strictly be written as P.B. (ΔP = Θ).
Back to General Report on Tunny. Contents.