General Report on Tunny
22X Page 76
22Y THE AMOUNT OF EVIDENCE DERIVED FROM A LETTER COUNT
The fundamental problem in chi-setting from a theoretical point of view is of the following type: given a ΔD letter count in which Θ occurs nΘ times, with 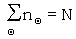 , to estimate the decibanage in favour of the Χ's being correct. The link and end being dealt with will be known always, the dottage (d) possibly. We will also have some prior knowledge of expected ΔD characteristics.
, to estimate the decibanage in favour of the Χ's being correct. The link and end being dealt with will be known always, the dottage (d) possibly. We will also have some prior knowledge of expected ΔD characteristics.
This knowledge can be expressed by saying that there is a probability Pi(∑Pi=1) for the theory, Ti, that the frequency of letter Θ in ΔD is
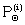 ; (Θ= /, 9, H ..., i = 1, 2, 3 ...). ; (Θ= /, 9, H ..., i = 1, 2, 3 ...). |
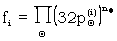 |
(Y1) |
This factor can be conveniently expressed in decibans of course.
Now, by the theorem of the weighted average of factors (see 21(1)), the factor in favour of the Χ's being correct is ΣPiƒi (Y2)
So we have a complete theoretical solution of the problem. The method could be made practicable for letter counts which are of a more or less standard type, but even for these, a great deal of preliminary statistical work would have to be done (R2 pp. 1, 59). If the letter count is not of a standard type it is tempting to use the Χ2 test. This has the disadvantage that the Χ2 test takes no account of which are the high-scoring letters and which the low-scorings ones. An attempt to overcome this objection is made in R5 pp. 1-4. This attempt is a theoretical formulation of what is really done in practice - namely the count is looked at to see if it is sufficiently 'bulgy' and then (slightly less important) to see if the bulges come at the right letters.
An alternative test which is quicker to apply, is the method of 'decibanning a letter count using the message as its own sample' (R4 pp. 56, 121). This method is obtained by writing, in (Y1), 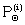 = nΘ/N.
= nΘ/N.
The decibanage given by this is
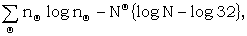 |
(Y3) |
When the logarithms are to base
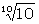 of course. It can be proved easily that this is equivalent to taking the maximum possible value of ƒi and therefore, by (Y2), the method is optimistic. It was designed originally as a method of rejecting seedy wheel-breaking stories. It is shown in R4, 121 that the decibanage will not be more the 80 d.b. too high.
of course. It can be proved easily that this is equivalent to taking the maximum possible value of ƒi and therefore, by (Y2), the method is optimistic. It was designed originally as a method of rejecting seedy wheel-breaking stories. It is shown in R4, 121 that the decibanage will not be more the 80 d.b. too high.
Back to General Report on Tunny. Contents.