General Report on Tunny
22X Page 74
22X THE ALGEBRA OF PROPORTIONAL BULGES.
(a) The Problem: Recovery of ΔP from ΔD.
It has been pointed out in 22H that the expected letter count of ΔD can be obtained from that of ΔP by means of the equations
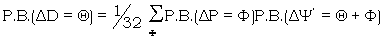 |
(X1) |
The problem of solving these equations for P.B. (ΔP) given P.B. (ΔD) led to the 'algebra of proportional bulges'. Even theoretically the problem is not simple, since the determinant of the coefficients vanishes. The advantage of using P.B.'s rather than probabilities is not great, but it does help a little. The reasons why proportional bulges were first introduced are mentioned in 21(J) (R1, 20).
(b) Application to Motor Runs.
The problem we are considering here as an application to the question of the expected score on a motor run (R5 23, 32). For we know that
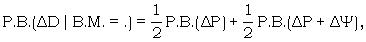 |
and the second term can be written as a 'Faltung', i.e. in a form similar to (1) above. When the limitation is Χ2 the count of ΔD against Χ2 = dot provides a sample of ΔD against motor crosses and we can therefore obtain a good idea of the L.C. ∝ ΔP and of the expected score in a motor run (R0 47-50). For limitations other than Χ2, the usual method was to assume 'flatness' of ΔP + ΔΨ in order to obtain a quick estimate (See chapter 23).
(c) Efforts at Solution.
The problem of solving equations (X1) for P.B. (ΔP) was first attached in R2, 69 where an erroneous connection with 'Fourier Transforms' was suggested. The theoretical aspects of the problem were pursued in R2 p. 87, 104; R3 pp. 24, 28, 32, 34, 37, 38, 48; R5 23 32; and a practical experiment in the solution of ΔP from ΔD is described in R3 pp. 71-3. Finally a relatively simple exposition of the whole subject was given in R5 59. In this chapter we give a still simpler account which contains all the essential ideas, with the introduction of the minimum of new notation. It will be observed that 'Fourier Transforms' are after all the simplest way of treating the problem.
(d) Exposition of the algebra.
Denote an arbitrary teleprinter letter by Θ or Φ. Let ƒ(Θ) be an arbitrary numerical function of teleprinter letters. The Fourier Transform
Back to General Report on Tunny. Contents.