General Report on Tunny
21 Page 42
success. Then the probability of exactly r successes is
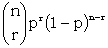 |
| If | |
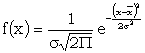
|
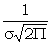 is the so called normalising factor which makes
is the so called normalising factor which makes 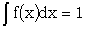 .
.
The integral of ƒ(x) is called the error function. A convenient way of tabulating this is in a deciban form. A table of Ψ(x) is given in R1, 109 where
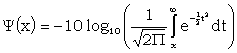 |
The binomial distribution is closely approximated by the normal one for quite small values of n, if we take x = pn and
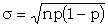 . In Tunny theory this is the most frequent form for σ. The normal distribution is also a good approximation when a variable is the sum of a lot of small independent contributions.
. In Tunny theory this is the most frequent form for σ. The normal distribution is also a good approximation when a variable is the sum of a lot of small independent contributions.
If the probability of exactly n successes is e-aan/n :, n is said to have a 'Poisson Distribution'. The formula is easy to remember since an/n! is a typical term of the expansion of an, so that
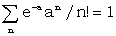 |
The binomial distribution is approximated by the Poisson distribution if n is fairly large but p is small, so that the average is much less than n. The Poisson distribution is approximated by the normal distribution when the number of successes minus a is small compared with a.
There is one other distribution used in the research logs, namely the 'Χ2 distribution'. Given n independent variables each with a normal distribution of mean 0 and S.D. 1, let Χ2 be the sum of the squares of these variables.
| writing | 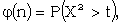 we have we have |
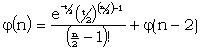 |
|
| where | 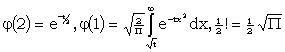 |
This is the most convenient formula when t is a good deal larger than n, as it is in all our applications.
Back to General Report on Tunny. Contents.