General Report on Tunny
21 Page 43
This distribution applies also to the sum of the squares of (n+1) such variables whose sum is fixed.
(m) Some simple formulae of a non-analytic type concerning proportional bulges.
If P and Q are independent propositions
P.B.(P.Q.) = P.B.(P) P.B.(Q) + P.B.(P) + P.B.(Q)
If Pi(i = 1, 2, ...) are mutually exclusive and exhaustive propositions each with the same 'random probability' then
 |
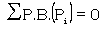If Pi (i = 1, 2, ...) are mutually exclusive propositions with the same random probability,
 |
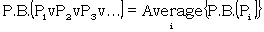If P, Q, Φ, Θ are teleprinter letters which have the same number of components, then
 |
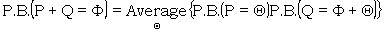(n) The general formula for sigma in Tunny work.
Let two tapes be compared, one with a proportion pi of letters Ai and the other with a proportion qi of letters Bi (i = 1, 2, ... r). Let the overlap of the two tapes be N.. Let the number of times Ai comes opposite Bi be υi. Let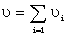 
. Then the average of υ is 
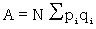and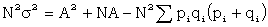 
.
| In particular, if r = 1 | |
| σ2 = Np(1-p)q(1-q). |
The proof of the general formula is best done by the method of characteristic functions. We do not describe this method here, but instead refer the reader to R4, 105-108.
(o) The statistician's fallacy.
A standard type of statistical experiment is exemplified by the following. A new fertiliser is tried and the amount of the crop produced is increased by 2σ. A deviation 2σ above the mean occurs about once in 40 experiments at random, assuming a normal distribution, and the result would probably be regarded as significantly good. As a conventional test of significance this is a useful method and one which is used in Tunny breaking also (as in the significance test for a short wheelbreaking run).
Back to General Report on Tunny. Contents.