General Report on Tunny

21 Page 41

case is sometimes referred to as the theorem of corrected excess.

(j) Theorem of the chain of witnesses (and 'proportional bulges').

A proposition which can either be true or false is handed on through a chain of witnesses of 'reliabilities' ½(1 + ζ_i) (i = 1, 2, 3, ...). (By reliability we mean here the probability of repeating what is heard instead of negating it.) Then the reliability of the chain as a whole is ½.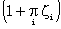

This theorem is the real reason why 'proportional bulges' were introduced. The 'Proportional bulge' or P.B., ζ, of a proposition is defined by saying that its probability is p(1 + ζ) where p is the probability that the proposition would have in certain conditions which in the applications can be described as a 'wrong case' or 'random case'. The theorem of multiplication of proportional bulges, given above, is true only when p = ½. There is a tendency for P.B.'s to lead to a slight algebraic simplification even if p ≠½.

(k) Expected value, standard deviation, variance, distributions.

Let a variable or 'variate' x have probability ƒ(x_i) of being equal to x_i. Then its expected value is defined as E(x) = Σx_iƒ(x_i). This is also called the mean (value) of x or the mathematical expectation of x or the average (value) of x. The average of the sum of two independent variables is equal to the sum of the averages, and similarly for the product.

The 'variance' of a variable is defined as the mean value of the square of the deviation of x from its mean. The positive square root of the variants is called the 'standard deviation' (S.D.) of x and is usually denoted by σ. Thus, if x is the mean value of x, then

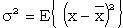
When we write x = x + σ we mean E(x) = x and S.D. of x is σ. There is no difficulty in extending the definition of an average to the case of a continuous variable.

If

P(x_i < x < x_i + dx_i) = ƒ(x_i)dx_i,

then

E(x) = ∫tƒ(t)dt

ƒ(x) is called the distribution function of x.

(l) Some special distributions.

Let n experiments be performed each with the probability p of

< previous

next >

Back to General Report on Tunny. Contents.

Back to The Enigma and the Bombe main page

Home

	If
		P(x_i < x < x_i + dx_i) = ƒ(x_i)dx_i,
	then
		E(x) = ∫tƒ(t)dt
	ƒ(x) is called the distribution function of x.