General Report on Tunny

22K Page 72

since the expected value of the modulus of the deviation from the mean is 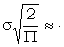so σ in the case of normal variate. Of course this is not accurate, but accuracy is not the point.

The expected sigma-age of a chi run (See 23C(d)) can be worked out sufficiently accurately from the average letter count, i.e. the 32 numbers nΘ. Some estimate of the S.D. of this sigma-age can be obtained from the numbers σΘ. A very crude method of doing this is given in R2, 56, 60, 61 and pp. 17, 21 of the note-book 'Alphabetical counts and runs statistics'.


22W   SOME FURTHER STREAMS

(a) The Sum of two P-Streams.

The frequency of letters in Pa + Pb is deducible from the frequency of letters in Pa by means of the Faltung Theorem (22E).

We can score a stream of letters suspected of being Pa + Pb. For each occurance of Θ in the stream we get a factor
   

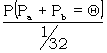that is a decibanage of 10 log 10 {32(Pa + Pb) = Θ}

 (W1)

The following table gives the centiban scores actually used in Room 41 for scoring suspected depths.

    Θ            Score     Θ            Score     Θ            Score     Θ            Score
    /             +31
    9                -1
    H             -12
    T              -16
    O              +7
    M              +1
    N             -17
    3              +4		     R             -15
    C               -1
    V              +7
    G              +2
    L             -24
    P               -4
    I                -1
    4            +10		     A               -2
    U             +11
    Q             -12
    W               -1
    5               +3
    8               +2
    K               -3
    J               +6		     D               -2
    F               +2
    X               -2
    B             -14
    Z               -4
    Y               -3
    S            +17
    E             -12

Fig. 22(XIV)


(b) The sum of two extended psi-streams.

Given two stretches of de-chi (a, b) which are known to have the same decode (as in an overlape) it is often possible to find the relative position of the P in the two stretches. For when set correctly
  ΔDa + ΔDb =  ΔΨ'a + ΔPa + ΔΨ'b + ΔPb
  =  ΔΨ'a + ΔΨ'b   (since ΔPa = ΔPb)

< previous

next >

Back to General Report on Tunny. Contents.

Back to The Enigma and the Bombe main page

Home