General Report on Tunny

22K Page 71

22J THE CIPHER STREAM



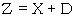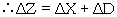	∴ Adapting (6a) and (6c) we get
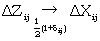		(J1)
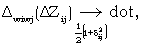		(J2)
	and in particular	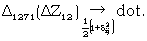(J3)

This formula has been used as the basis of a formula for determining whether unidentified traffic is on Tunny, (See R3 p. 77) and the discussion on Significance test Θ in Ch. 24.

22K SAMPLING ERRORS IN ALPHABETICAL COUNTS

Our knowledge of alphabetical counts of ΔP and ΔD is essentially empirical. There is no very exact knowledge of what a ΔP count should look like, even for a given end of a given link, since the count depends on the particular operator and the context of the message. The factor which a supposed ΔD count gives, in favour of the de-chi being correct, is discussed in 22Y. Here we discuss shortly the method of obtaining typical counts.

Suppose we have r samples, all the length 3200, of ΔD for a particular link and the value of d. It is so convenient to be able to work with the average of these counts that we normally do so unless there is too obviously more than one type of language represented. Suppose the numbers of occurrences of Θ in the samples are

n⁽¹⁾_Θ, n⁽²⁾_Θ, ..., n^(r)_Θ.

The obvious thing to do is to take the number of occurrences in a typical example as

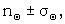where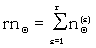

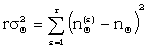(K1)

In order to estimate σ_Θ it is easier to calculate 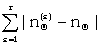, which can be done in a self-checking way, and to write

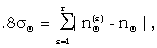(K2)

< previous

next >

Back to General Report on Tunny. Contents.

Back to The Enigma and the Bombe main page

Home

n⁽¹⁾_Θ, n⁽²⁾_Θ, ..., n^(r)_Θ.
The obvious thing to do is to take the number of occurrences in a typical example as

where
		(K1)