General Report on Tunny
24X Page 146
where the summation is over all wheel patterns defined as substantially the same as those of the rectangle. This formula is equal to
 |
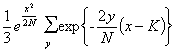where K is some sort of mean value of y for substantially equivalent patterns. We assume further that y is the sum of any number of terms y1, y2, ... which are the moduli of the x's. It might be objected that this includes values of y that are too large to be permitted for substantially equivalent patterns, but then the terms with large values of y are negligible anyway.
This makes the factor
 |
|
 |
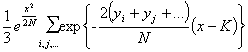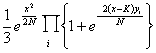Expressed in decibans, this gives, allowing for the prior odds
 |
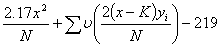where
| ζ(a) = 10log10(1+e-a). |
The formula is now suitable for numerical calculation provided some value of K can be decided upon. It is just this part of the problem which is the least important though it is the most difficult. Let the pippages of the ΔΧ1 on the rectangle be a1, a2, ... , a4, and let any other pattern be put into correspondence with pippages which are the same as the ai's at places where the wheels are the same and are -ai at places where they are different. We can then say that the wheel patterns are substantially equivalent if these two sets of pippages score positively against each other when scored on the wheel-sliding table. It can be shown (see Black File) that if the message is not too short this definition leads to a maximum value of y of about 432. This is the origin of the usual value of K, namely 216. A rival value for K is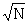 
(see R3 pp 117, 118, R4 p 38) and in any case K must be taken as a function of N in order t cope with key rectangles. As a rough judgement based on experiences, K = 1.3 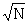seems fairly good. Observe that every zero scoring character contributes a factor of 2. This is exactly right because the character can be taken as a dot or a cross without affecting the double bulge, so the prior probability of the wheel patterns permitting the double bulge of z is 2 x 2-71 instead of 2-71.
Back to General Report on Tunny. Contents.