General Report on Tunny
24X Page 143
obtained in which the double bulge x is greater than or equal to x*. The true value of δ is approximately x*/N (see R3 pp 68, 87). The difference x - x* is something like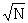 
(R3 pp 117, etc.). This estimate depends on the assumption that the final convergence gives wheels that are substantially correct and this is the question we are going to consider here. We begin with three significance tests which have a certain weakness in common and then describe a fourth test which is relatively free from this weakness.
I. We may try to use the value of a pip to estimate the factor in favour of the wheel patterns being substantially right. If we say that the rectangle is x half pips up we get a decibanage of roughly 2.17xx*/N.
II. This expression is very sensitive to the exact estimate of x*. Suppose we imagine δ = 0 and assume the distribution of x is normal. Then the probability that x will reach a specified value is roughly
 |
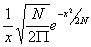We should like this to be less than 2-71, since 2-71 represents the prior probability of the wheel patterns assumed (71 = 41 + 31 - 1). (One is subtracted because two theories for which the wheels are relatively inside out are equivalent).
III. There is a method called the square summing of columns, described in R1 p 95, which is more rigorously provable than II but is more trouble to apply. (Also it sacrifices some of the evidence, unless the rectangle is exactly 1271 long) (See R2 p 15.)
In the three methods described above it is implicit that there is a prior probability of 2-71 to be offset, or a decibanage of 214. But really it is not as bad as this, because we are interested only in the wheels being substantially right, and the number of wheel patterns which can be regarded as substantially the same as the converged rectangle wheels may be quite large. In this sense the tests II and III are too harsh, but in another sense they are too lenient, namely in the sort of way that the glib use of the error function is too lenient when setting chi's. (See chapter 21(o) 'Statisticians' Fallacy'.) On the whole it seems best to make a direct appeal to Bayes' theorem.
Back to General Report on Tunny. Contents.