General Report on Tunny
24W Page 131
and this is symmetrical with respect to the two wheels. If the message were de-chied with the wheels consisting of the final patterns then X = the double bulge of the 1p2 score (provided that places where the differenced wheels are doubted are not included in the count).
The formula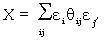 
is true at all stages of the convergence and the effect on the wheel patterns of the progress of convergence is the same as first choosing the numbers ε1, ε2 ... so as to maximise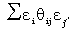 
(leaving ε1, ε2, ... unchanged) and so on. Clearly X must keep on becoming larger and larger until it reaches a maximum value, when the rectangle is converged.
If the phrase 'crude convergence' is interpreted in a more up to date sense, in which characters may be doubted if their scores in pips are low (or on grounds of unfavourable wheel characteristics), then it is no longer essential that X should continually grow (see R2 pp 9, 11). However it was always the practice to complete the convergence (i.e. to get complete patterns) in order to get a check on the sum of the moduli of the pippages of the two wheels.
The mathematical description given above applies to the hand process of crude convergence and to the Colossus process of convergence of a rectangle. The two processes are of course equivalent.
The reason for the adjective 'crude' is that there is another method called 'accurate convergence', in which
|
|
|
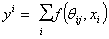
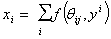
where ƒ(k,l) is a symmetrical function of k and l. It will be seen that the exact magnitude of the pippages of the wheel taken through are used, instead of their sign. The function ƒ(k,l) is defined as
|
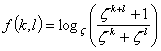
where
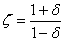
and (see R1 pp 37, 43, 45, 49) a conventional value of δ is assumed. A table of ƒ(k,l) can be conveniently constructed by means of a specially made cardboard slide-rule, in view of the identity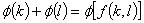 
where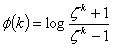 
.
Back to General Report on Tunny. Contents.