General Report on Tunny
23d Page 82
BR 3407 0450/24/2 WD 23/2 COL 7 T 6020 1P2/L R 3106 A 1553 Φ 27.8 ST 1624 K1 K2 02 08 E 1631 02 20 E 1625 11 09 A 1633 16 07 A 1629 18 08 D 1629 19 31 C 1625 37 21 E 1637 40 28 B 1655 B 102 3.7Φ 40 28 C 1655 SET K1 K2 40 28 SPAN IN 1000'S 0271 0245 0268 0249 0301 0214 0280 0237 0268 0247 0261 0257 SPAN 4000-END IN 500'S 0139 0119 0129 0128 0131 0128 0130 0129 SPAN 01-4500 1259 1064 2B 195 B 98 4.1Φ SPANNING 01-4500 SET K1 K2 40 28 GOOD |
The items in the first line are message number, time and date sent, wheel day and Colossus number. T 6020 is the text length, measured as a check, as soon as the tape is on Colossus. 1P2/L is typewriterese for 1+2/ Χ2 x; this run is chosen because the chit (not preserved) was so marked [23E]. R 3106 is the number of places looked at, i.e. the number of places where Χ2 = x. At random the expected number (A) of these when 1+2 = . is ½ × 3106 = 1553. Φ (typewriterese for σ) 27.8 is the standard deviation of 1+2 = . viz. ½ 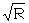 = ½ = ½ 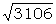 . This is of course an application of the formula quoted in 21 (b), that if random proportional frequency in a normal distribution is p, the standard deviation is . This is of course an application of the formula quoted in 21 (b), that if random proportional frequency in a normal distribution is p, the standard deviation is 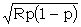 . A table of ½ . A table of ½ 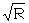 and ¼ and ¼ 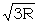 is provided at each Colossus. is provided at each Colossus.ST 1624 is the set total, i.e. Colossus is set so as not to display or print any smaller score. Because this is a two-wheel run, ST is taken as A + 2½σ. The best score is 3.7σ, not even "good" [23C(a)] but worth spanning [23F(o)]. In each pair of span scores the upper is 1+2 = ., the lower 1+2 = x : this makes it easy to see where a slide occurs, evidently between 4000 and 5000, for 5000 - 6000 shows almost no bulge and 4000 - 5000 only a small bulge. 4000 - 5000 is therefore spanned in 500's and the bulge of 1+2 = . is seen to cease at about the 4500th letter: it is therefore believed that there is a message slide here and the subsequent runs are done spanning 1 - 4500: the sigma-age is now 4.1 instead of 3.7; the setting is therefore "good". Here the operator makes the mistake of neglecting a 4-letter count for ΔD1, ΔD2 [23E(h)] this is easily reconstructed and would read . . 592 . x 498 x x 667 x . 567 Because xx is so strong, this would have suggested the run 3+4x/1x2x which would in fact yield a score of 7.9σ. |
Back to General Report on Tunny. Contents.