General Report on Tunny
23C Page 80
"certain" or "good" setting. See 23C(a). The runs for the last wheel should be "certain". If all these fail, the message is abandoned, unless it is to be flogged (23 J).
(ii) ΔD is omitted and only the suffixes denoting the impulses are written: this is the invariable custom. (R0 p. 110).
(iii) Impulses to the right of the oblique stroke are supposed already set.
(iv) The Break In is the initial run used when setting a message (which has nothing to the right of the oblique stroke).
(v) "Span" is in the diagram,because, as soon as the first wheels are set, the message is invariably spanned for possible message slides (See 23 F).
(See also R3 p. 134; R4 p. 7;R1 p. 99; R2 pp. 42, 44, 48.)
(d) More powerful methods.
Though the above tree will suffice to set a large proportion of messages, it is rather crude. Having already set several recent messages on the same link, one would probably introduce a few modifications.
For the best results messages on Χ2 limitation may require a quite different break-in. (23 E)
Other runs are mentioned in 23 J: R1 is full of much references; recent notes include R3 p. 131, R5 p. 106.
23C WEIGHING THE EVIDENCE
(a) Sigma-age.
The bulge of a score is its excess over random.
The sigma-age is the ratio of the bulge to the standard deviation for random scores: it is a measure of the improbability that the sum will occur at random in a single trial, i.e. at a particular setting. If many settings are tried, the improbability will be proportionally reduced. In one-wheel run the number of settings tried lies between 23 and 41, in a two-wheel run between 598 an 1271 and so on.
This improbability that a score will have occured at random is clearly some indication of the degree of certainty that the corresponding setting is correct. Unless there are rival settings the following table is used.
| Number of wheels set by the run | 1 | 2 | 3 | 4 | 5 | |||
| Sigma-age |  |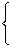
for a "certain" setting i.e. odds 50:1 on | 3.8 | 4.5 | 5.2 | 5.8 | 6.4 | |
| for a "good" setting i.e. odd 6:1 on | 3.2 | 4.0 | 4.7 | 5.4 | 6.0 |
The formula for sigma is
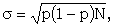where p is the random proportional frequency [21 (K)]. In Χ-setting p is almost always 
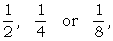giving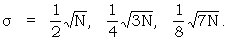 
Back to General Report on Tunny. Contents.