General Report on Tunny
22H Page 69
Putting j = 6 δi6 = Πi6.β
| ∴ PB(ΔDi + lim = cross) = Πi.β | ||
| ∴ (for Χ2 = lim) | PB(ΔD2 + 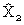 → x) = Π2.β → x) = Π2.β |
(H9) |
| Now |
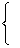 |
[illegible] → dot (nearly always) | |
| [illegible] → cross (for punctuation) |
| ∴ | ΔD2 → dot | ||
| ΔD2 + Lim → dot (R1 p. 9) | (H10) |
Figs. 22 (VI)(VII)(VIII) give scores [illegible] for the various ΔD counts shown.
The following table gives values for two impulse ΔD proportional bulges against limitation dots and crosses.
| δ..≡ | PB(ΔDi = . ΔDj = . | L = .) | ||
| δ..≡ | PB(ΔDi = . ΔDj = . | L = x) | ||
| δ..≡ | PB(ΔDi = . ΔDj = .) | and so on |
|
Fig. 22(XII)
The workings are left to the reader (similar workings are given on R4 p. 80)
Two results should be noticed.
(i) δ.. = δxx and δ.x = δx.. Whatever the relative values of Π.. and Πxx. This shows that the benefits of counting against Χ2 limitation
Back to General Report on Tunny. Contents.
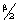 {β(Π.. + Πxx) - β(Π.. - Πxx)}
{β(Π.. + Πxx) - β(Π.. - Πxx)}