General Report on Tunny
22G Page 65
Except when a message consists almost exclusively of German language, the best ΔPij bulge is on ΔP12 → dot. On German language, the bulge on ΔP12 → dot is weak (though usually positive) and the best bulges are on ΔP34 → x and ΔP13 → dot. See Fig. 22(x)
| PB (ΔPi = dot) is defined as Πi |
| PB (ΔP = Θ) is defined as ΠΘ |
(f) Δ2P.
A Δ2P letter count and the corresponding ΔP count is given in R3 p. 86. The bulginess of Δ2P is the more marked, the frequency of U being about 8% and O S M 3 4 all occurring over 5% of the time. (R0 p. 50.)
(g) Bigrams in P and ΔP.
Fig. 22 (IV) gives a table of Bigram frequency in P.
No statistics of ΔP bigrams were taken.
(h) The sum of two P streams.
By considering the frequency of letters in Za + Zb for two messages (a, b) alleged to be in depth it is sometimes possible to decide whether Za + Zb = Pa + Pb and the messages are infact in depth or not. A Scoring table for alleged depths is given in 22 W(c).
22H THE DECHI STREAM
| D = P + Ψ' | ∴ ΔD = ΔP + ΔΨ' |
The undifferenced Ψ' stream is flat, therefore the undifferenced D stream is flat and unrecognisable statistically. [(E3).]
(a) Frequency of letters in ΔD.
| Applying (E1) and (E2) we get | ||
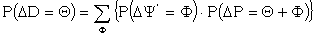 |
(H1) | |
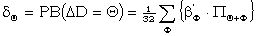 |
(H2) |
The most important contribution to the frequency of any letter Θ in ΔD comes from the proportion of places in which there is a Θ in ΔP and a stroke in ΔΨ'. Now P(ΔΨ' = /) = (1 - a) + a(1 - b)5 = approx. (1 - a), and (1 - a) varies in value from .18 when there are 14 dots to .38 when there are 28 dots.
As a result, 1/5 - 2/5 of the ΔP stream is reproduced exactly in the ΔD stream, and, assuming (as a first approximation) that ΔD is flat when ΔΨ' ≠ /, we can see how ΔD count can be thought of as a ΔP count "watered down" by the addition of random material from the places where
Back to General Report on Tunny. Contents.