General Report on Tunny
22D Page 51
limitations.
The following table gives the frequency in ΔΨ' of each '6-impulse letter'.
|
Fig. 22(III) |
| From this table we see that | P(ΔΨ' = 9, L = .) | |
| = | P(ΔΨ' = N, L = x) = ab2(1-b)4 | |
Fig. 22(V) shows ΔΨ' letter counts for Ψ' streams corresponding to d = 27, 24, 21, 18, 15. ΔΨ' counts are given separately for Χ2 lim and Χ2Ψ'1 lim, and in the case of Χ2 lim the counts of ΔΨ' against L = x and L = . are given separately.
An immediate application of the ΔΨ'6 principle to (D7) gives
ΔΨ'i + L 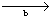 x x |
(D8) |
(h) Proportional bulges of letters in ΔΨ' stream.
The proportional bulges of (ΔΨ = Θ) (ΔΨ'= Θ) where Θ is any letter, are denoted by βΘ, β'Θ and PB's (ΔΨij = dot) and (ΔΨ'ij = dot) by βij, β'ij.
A table similar to Fig. 22(III) showing PB (ΔΨ' = Θ) for all values of Θ in terms of β is given in R5 p. 27.
| P(ΔΨ'ij = dot) = ½(1 + β'ij) = b = ½(1+ β) | ||
| ∴β'ij = β | (D9) |
The idea of a PB and the introduction of β first occurs on R1 p. 20.
(i) Δ2 characteristics.
It is a fairly good approximation to accept the simple minded results
| Δ2Ψi →. with probability b2 + (1 - b)2 = 2b2 - 2b + 1 | |
| Δ2Ψ'i → . with probability ½ | |
| Δ2Ψ'ij → . (see R3 p. 22). |
(j) The sum of Psi streams.
It is sometimes useful to be able to recognise statistically
Back to General Report on Tunny. Contents.