General Report on Tunny
21 Page 39
 |
||
 |
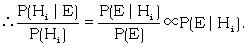A special case of Bayes' theorem, itself often referred to in the research logs as Bayes' theorem, is particularly important in cryptographic problems. Suppose we consider the hypotheses H and 
. Then, by the theorem above
 |
||
 |
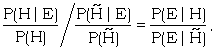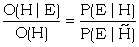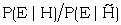is called the factor in favour of H given E, and is seen to be the factor by which the 'prior odds' O(H) must be multiplied in order to get the 'posterior odds' O(H|E). In the more general form of Bayes' theorem any set of numbers proportional to P(E|Hi) can be called the 'relative factors' in favour of the various hypotheses Hi and they are the ratios by which the prior probabilities may be multiplied, in order to get the correct ratios for the posterior probabilities. The special case of Bayes' theorem was first used in B.P. by A.M. Turing. (The fact that it was a special case of Bayes' theorem was pointed out by I.J. Good.)
(g) The deciban.
But Turing's great advance consisted in the invention and application of the 'deciban' (in Hut 8). (Deciban is abbreviated to 'd.b.'.)
This is defined simply as 10log10ƒ, where ƒ is the factor as defined above. Simple though this idea is, it makes an enormous simplification in practical work. As an example let us suppose that a penny is tossed 20 times and that each time it comes down heads. Suppose that we have two theories (i) that the penny is unbiassed, (ii) that it is double headed, and suppose that the second hypothesis (H) has prior odds of one in ten thousand. If we call E the event that the coin comes down heads then
 |
||
 |
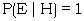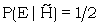Therefore the factor in favour of H given E is 2, i.e. 3 decibans. So we gain 3 x 20 = 60 decibans from the whole series of experiments. The prior odds were 1/104 i.e. 40 d.b. down and so the posterior odds are 60 - 40 = 20 d.b. or 100:1 on. (Observe that we talk about the decibanage of 'Odds', meaning, of course, 101og10o.)
Back to General Report on Tunny. Contents.