General Report on Tunny
11B Page 6
Before considering in detail the operation of the Tunny machine it is necessary to define the addition of two teleprinter letters.
Teleprinter letters are added by summing corresponding impulses according to the rules

Therefore 9 + Y = 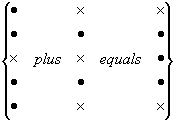 = Z
= Z
From this example it is clear that not only 9 + Y = Z but also that 9 + Z = Y and Y + Z = 9. This is an important result which may be stated in the form of the theorem: Addition and Subtraction of teleprinter letters (or characters) is the same thing. (A1)
Any proof required is left to the reader.
Fig. 11 (I) shows an addition square giving the sum of every pair of letters.
(b) Tunny Key.
For each letter in turn of the unciphered stream of impulse signals, the Tunny machine makes up a key-letter (K) and adds it to the plain text (P) to get a ciphered letter (Z).
The P-stream can contain any letter of the teleprint alphabet except /, 3, or 4. Of the letters that do occur 9 (space), 5, 8, and E are particularly common. The K-stream, and therefore Z-stream, contains each letter of the teleprinter alphabet approximately an equal number of times.
| Example | P-stream |
|
||||||||||||||||||||||
| K-stream |
|
|||||||||||||||||||||||
| Z-stream |
|
(c) The Wheels.
12 wheels are used to generate the key. Each wheel consists of a pattern of dots and crosses of a given length. Each character moves into the active position in turn, and when the wheel has gone round completely the pattern is repeated. The wheels are divided into three groups with the following names and lengths.
| CHI (Χ) Wheels | Χ1 length | 41 characters |
| Χ2 | 31 | |
| Χ3 | 29 | |
| Χ4 | 26 | |
| Χ5 | 23 | |
| PSI (Ψ) Wheels | Ψ1 length | 43 characters |
| Ψ2 | 47 | |
| Ψ3 | 51 | |
| Ψ4 | 53 | |
| Ψ5 | 59 | |
| MOTOR or MU (μ) Wheels | μ61 length | 61 characters |
| μ37 | 37 |
Back to General Report on Tunny. Contents.