Cryptographic History of Work on the German Naval Enigma
running and 1 has the excellent feature that Y = T + 6 is "picked up" i.e. appears in the alphabet as a result of reciprocal values; the denial of A = Y + 3 (this would give A/A which is impossible) is not very serious as this is not much better than an even chance anyway. Let us consider this alphabet further
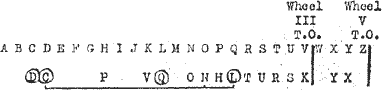
Q = S + 17 gives Q/L and L = C + 13 this gives C/D, so these letters have
been put in ringed. If this alphabet is right we can discover something about
the wheels in the machine. (1) Since RWL = RWC + 0.13 the end
wheel does not turn over the middle wheel in this stretch of 13 letters i.e.
there is no turnover from D to Q. Similarly there is no turnover from O to
V (from STK = STN + 0.7)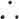 
The turnover comes between V and D. That only leaves wheel III (V/W) and V
(Z/A) possible.
16. We may now (1) test the correctness of the part of the alphabet we have obtained and (2) clean up whether it is wheel III or wheel V by turning to the deciban sheets recording end wheel comparisons and picking pairs of messages there with end letters known. Suppose,
Our alphabet says T = H + 2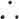
We must take the entry corresponding to that, marked with an arrow 
and this gives a "score" 
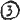or + 3 in favour
of the alphabet. Suppose our total list of scores accumulated in
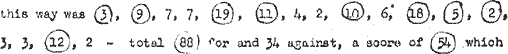
improves the alphabet by a factor of 500 and makes it virtually certain to be right.
17. Now suppose we have a comparison between AJY and AJD; if the right hand wheel is wheel V AJY = AJD + 21 as there is no turnover in the
-101-
Back to Cryptographic History of Work on the German Naval Enigma contents