Cryptographic History of Work on the German Naval Enigma
14. From this list we can make up a "chain" as follows. Since ARX = AYR + 6.5 X must be 5 places ahead of R in the alphabet i.e. when the "right hand wheel alphabet is written out as in Para. 2 they must be place R .... X. Since VRN = VXR + 0.21 N is 21 ahead of R i.e. R is 5 ahead of N; also K is 7 ahead of N, K is 14 ahead of P (or P is 12 ahead of K) and P is 15 ahead of U (or U 11 ahead of P - we can look at it either way). The chain showing the relative positions of the encypherments of these 6 letters is
P. . . . . . N . . . U R . K . . X . . . . . . . .
15. Now we will try to find their actual values, trying P = A, B, C .... Z in turn and seeing what values this gives us for the other letters. The simplest way of doing this is to write out the alphabet and "slide" the letters of the chain underneath keeping them the right distance apart - a process known to us as "scritching".
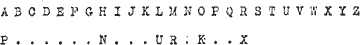
Since the machine is reciprocal, the assumption A encyphers as P [written
A/P here for short] implies P encyphering as A; similarly H/N gives N/H, L/U
gives U/L and M/R gives R/M. This last consequence however is impossible as
we already have R/X 
The assumption A/P
is wrong. Eliminating impossible tries like this as we go along we get left
with
The fits L = C + 13 (6 : 1 on), Y = T + 6 (5 : 1 on), A = Y + 3 (3 : 2 on) and Q = S + 17 (50 : 1 on) have not yet been used and we are now able to employ them in further testing. Alphabets 2 and 3 do very badly testing in this way; neither L = C + 13 nor A = Y+ 3 can be fitted into number 2 and Q = S + 17 will not fit into 3. This leaves 1 and 4 in the
-100-
Back to Cryptographic History of Work on the German Naval Enigma contents