Turing's Treatise on the Enigma
Each of the 263 trigramme must occur equally often on cards in
this urn, and must of course have with it the number of previous occurrences
of this trigramme. Now imagine that we have worked out a certain number of
V.K.G. using a given bigramme table, and that we have found out how many times
each of them had occurred before. This can be compared with being given one
of the urns, and told "It is Q:1 on this being the random urn",
and then drawing a certain number of cards from the urn. After the draw we
have a new idea of the odds that the urn is the random urn, and we should
have a correspondingly modified idea of the odds that the bigramme list is
the right one. Let us suppose that the trigrammes, in the order as they were
worked out, had the numbers r1, r2, ... r5
of previous occurrences, and that correspondingly the cards drawn from the
urn bore the numbers r1, r2, ... r5. The
proportion of cases of draws of s cards from the urn, giving these results
with the same order, is ur1, ur2,
... ur5 where ur is the proportion of r-cards
in the urn.
Likewise the proportion of cases where this happpens with the other urn is
ur1', ... ur5' with a corresponding meaning
for ur'. Then the odds on the urn not being the random one after
the experiment are

In other words the drawing of a card with the number r m improves the odds by a factor of
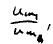
which is equal to
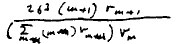
except in the case m=0 when it is
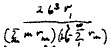
The same method may be applied for the identification of some unknown bigrammes
By taking into account a number of days traffic all using the same bigramme
table we may find a number of indicators whose V.K.G. would be completely
known if we knew the value of a certain bigramme. If we make the right hypothesis
as to the value, we should get trigrammes agreeing with the ststistics as
before. In this sort of case, as the data is liable to be very scanty, it
is essential to use the accurate theory as described above.
-144-
Back to Turing's Treatise on the Enigma. Chapter VII.