On the basis of thorough and repeated investigations, [Enigma has] proved itself … unbreakable.
Rear Admiral Ludwig Stummel
Since any one of the five rotors could be placed in the left position, any of the remaining four could be placed in the middle position and any of the remaining three could be placed in the right position, there were 5 x 4 x 3 = 60 possible ways of selecting and ordering the rotors.
Each of the rings around each rotor could be placed in any one of 26 positions, known as the Ringstellung, or ring setting. So there were 26 x 26 x 26 = 17576 possible ways of rotationally positioning the rings around the rotors. From the cryptanalytical viewpoint the Ringstellung on the left rotor was irrelevant because its turnover notch did not affect other rotors, so the real contribution of the Ringstellung to the complexity of the Enigma was 26 x 26 = 676 positions.
Once clamped in the Enigma each of the three rotors could be rotated into any one of 26 positions, so there were 26 x 26 x 26 = 17576 possible ways of rotationally positioning the rotors in the machine.
By far the greatest contribution to the complexity of the Enigma was the stecker. Using all ten leads there were over 150,000,000,000,000 ways of plugging up the steckerboard. German cryptanalysts believed that this huge number would guarantee the security of the Enigma. They were wrong.
The total number of states of the Enigma was therefore:
60 x 17576 x 676 x 1.507382749373 x 1014 = 1.074586873273 x 1023
The task of the cryptanalyst was to determine which one of this tremendous number of states (more than one hundred sextillion using the American system of naming numbers), was used as the key for that day.

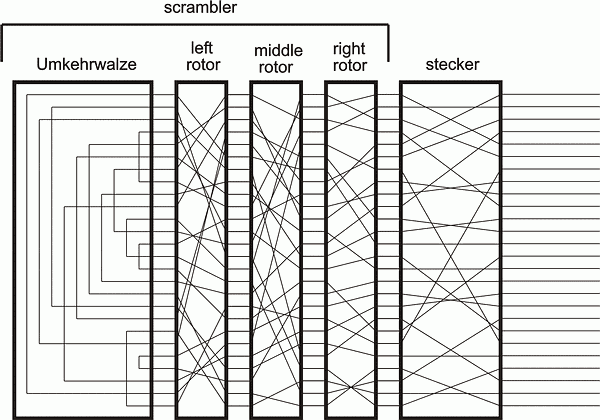
It can be seen from Figure 2.1, the logic diagram of the Enigma, that the Umkehrwalze prevents the Enigma from enciphering a letter as itself, that is, it can never encipher R as R, or J as J, and so on. This proved to be a crucial defect of the machine.
It also can be seen from Figure 2.1, that with two identically set up Enigmas, if, say, F was pressed on one machine and T was illuminated; then pressing T on the other machine would illuminate F. In other words, the Enigma is reciprocal, that is, the ciphertext of any plaintext enciphered on one Enigma, will, when keyed into an identically set up Enigma, yield the plaintext. So the receiving operator had merely to set up his machine in accordance with the instructions for that day.
Copyright © Graham Ellsbury 1998
Continue to The Turing Bombe Part 1. Cribs and Menus
Return to The Enigma and the Bombe main page